1 > 0 → U(t, r, v, d, e, ψ, ∂ψ, ...) = 1/T(t, r, v, d, e, ψ, ∂ψ, ...) > 0;

2) The joint isotopic lifting of the conventional 20th century associative product AB between generic quantities A, B (numbers, functions, matrices, operators, etc.) into the associative preserving form

AB → A∗B = ATB; under which

3) Under which U is indeed the left and right multiplicative unit at all levels

U∗A = A∗U = A for all elements A of the set considered.

IsoMathematics was conceived and mostly developed by the Italian American scientist Ruggero Maria Santilli (see his curriculum) in the late 1970s when he was at the Department of Mathematics of Harvard University under support by the U. S. Department of Energy. The studies on Santilli's IsoMathematics have then been continued by various mathematicians and physicists.

It is evident that the isotopic lifting of the basic multiplicative unit and of the related associative product require the systematic, step-by-step compatible lifting of the entire 20th century mathematics over a numeric field. Among rather vast studies done to date, we mention Santilli's invited talk at 2012 ICNAAM [1] and specialized studies on: isonumbers [2,-4]; isospaces [5]; isofunctional analysis [6]; isodifferential calculus [7]; iso-Lie theory [8,9]; iso-Hilbert spaces [10]; isotopology [11]; general review [12]; and independent review [13].

Santilli's Regular IsoMathematics [13] can be easily constructed via a nonunitary transformation applied to the "totality" of quantities and their operations of 20th century mathematics. In fact, for any given isotopic unit U there exists a nonunitary transform WW⁺ = U ≠ I, under which

W 1 W^† = U, W (AB) U^† = A'∗B', A' = WAW^†, B' = WBW^†,

and the same lifting applies to derive all other quantities and operations of Regular IsoMathematics.

Santilli's Irregular IsoMathematics [13]. by contrast, cannot any longer be constructed via nonunitary transforms of conventional mathematics and constitutes a truly new field of mathematics. As an illustration, the structure constants of Lie's theory are preserved under lifting to the Regular Lie-Santilli isotheory. However, in the transition to the Irregular Lie-Santilli isotheory, the structure constants become "structure functions" and, as such, they cannot any longer be constructed via nonunitary transforms of structure constants.

Additionally, 20th century applied mathematics solely admits a meaningful conjugation from matter to antimatter at the operator level (namely, the quantum mechanical charge conjugation on a Hilbert space defined over a field of complex numbers), which admits no image in classical mechanics. The consequence of this limitation is that Einstein's special and general relativities cannot represent a "neutral" antimatter body, since the sole available conjugation is that of the charge. Following additional decades of studies, this insufficiency has been resolved by:

Santilli IsoDual Mathematics [13.14] which is characterized by an anti-Hermitean transform of conventional and isotopic mathematics applied to the totality of quantities and their functional dependence, e.g.,

Q(t, r, v, d, e, ψ, ∂ψ, ...) → -Q^†[-t^†, -r^†, -v^†, -d^†, -e^†, -ψ^†, -(∂ψ)^†, ...]

as well as to all their operations. When applied to a classical formulation, such as the Riemannian representation of gravity, the above isodual conjugation has indeed permitted the achievement for the first time of an axiomatically consistent representation of the gravity of neutral, as well as charged, antimatter bodies, while at the operator level the isodual map coincides (by construction) with the conventional charge conjugation [14].

As predictable from its novelty, IsoMathematics has permitted intriguing new discoveries, such as the quantitative prediction and experimental verification of: anomalous frequency shifts of light within physical media without relative motion between the source and the observers, known as Santilli IsoShifts [15]; a new chemical species with bonds weaker than the valence, thus permitting new fuels without contaminants in the exhaust [16]; the Intermediate Controlled Nuclear Fusions without radiations [17]; and other basic advances (see the general review [19]).

THE NEED FOR ISOMATHEMATICS
As it is well known, 20th century mathematics provides an excellent representation of "exterior dynamical systems" (point particles and electromagnetic waves propagating in vacuum), since these systems do admit a local-differential topology. Santilli proposed IsoMathematics for the treatment of the broader "interior dynamical systems" (extended particles and electromagnetic waves propagating within physical media), because conventional mathematics is no longer applicable to the latter systems due to the emergency of nonlinear, nonlocal and non-Hamiltonian effects. Additionally, IsoMathematics is rendered necessary by the known No Reduction Theorems that prohibit a consistent reduction of interior dynamical systems to a finite number of isolated point-particles in vacuum.

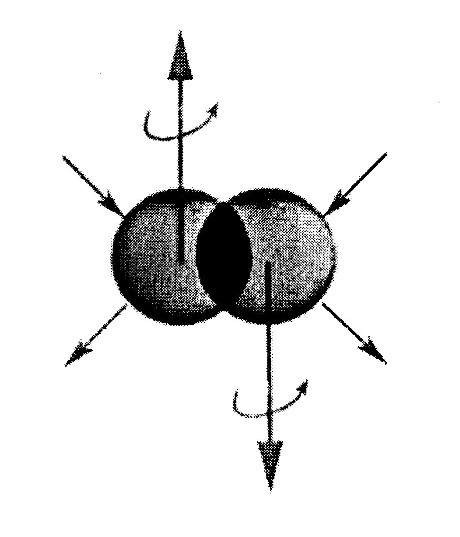
Experimental evidence has established that molecular binding energies have large values originating from pairs of valence electrons in singlet coupling. But electrons should repel each other according to quantum mechanics and chemistry because they are assumed as being point-like charges. Santilli has indicated repeatedly that, even though point-like charges do exist, "there exist no point like wavepackets in nature." The admission that electrons have an extended wavepacket implies the inapplicability for their singlet valence couplings of virtually the entire 20-th century mathematics, physics and chemistry since there is the emergence of nonlinear, nonlocal and non-Hamiltonian (variationally nonselfadjoint [12]) forces beyond any dream of treatments via said 20th century formulations. Santilli isomathematics and consequential isotopies of quantum mechanics and chemistry, called hadronic mechanics [13] and hadronic chemistry [20], have resolved the indicated basic insufficiency of 20th century chemistry, by achieving exact representation of molecular binding energies from unadulterated first principles, while permitting the development of new technologies and industries [20].

Among examples in quantitative sciences ranging from Newtonian mechanics to biology, a clear illustration of the need for IsoMathematics is given by the synthesis of the neutron from a proton and an electron in the core of a star. Since the neutron is 0.874 MeV heavier than the sum of the rest energies of the proton and the electron, the use of conventional Hilbert spaces over a conventional field of complex number is "inapplicable" (and not "violated" because it was not conceived for that), In fact, Schrodinger's equation

H(r, p) ψ = [p²/m - V(r)] &psi' = E ψ

is physically consistent for all bound states having a "mass defect" or, equivalently, requiring a "negative binding energy," as it is the case for nuclear, atomic and molecular bound states. By contrast, the synthesis of the neutron from a proton and an electron would require a "positive binding energy," under which Schrodinger's equation no longer admits physically consistent solutions.

By contrast, the use of IsoMathematics, with particular reference to the Schrodinger-Santilli isoequation

W[H(r, p) ψ]W^† = H'(r, p) T(ψ', ∂ψ', ...) ψ' = E'ψ'

has permitted Santilli to achieve the "exact" relativistic representation of "all" characteristics of the neutron in its synthesis from a proton and an electron inside a star (and not just the representation of the neutron rest energy), with a corresponding exact relativistic representation achieved via the Dirac-Santilli isoequation (see the review [18]).

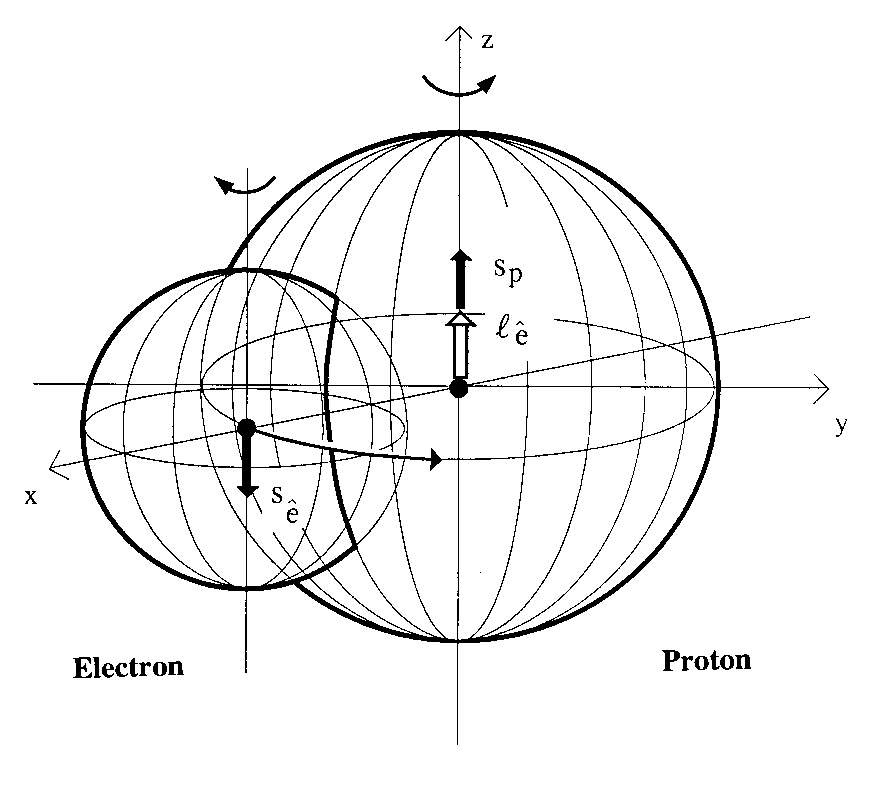
Quantum mechanics can only represent protons and electrons as point-like particles, by therefore resulting in the complete inabilty to represent the synthesis of the neutron inside stars, p + e => n + v, due to the need for a "positive binging energy" (since the rest energy of the neutron is 0.784 MeV bigger than the sum of the rest energies of the proton and the electron), with ensuing catastrophic inconsistencies. Santilli has achieved the first and only known axiomatically exact and time invariant representation of "all" the characteristics of the neutron in its synthesis inside stars from protons and electrons for which very reason he conceived and developed isomathematics and the related isotopies of quantum mechanics (for a freviuew of thgis 30 years long scientific journey, see reviews [118,19]). Note that the admission of the proton as an extended particle implies the emergence of an angular mo,mentum of the electron when totally immsersed inside the proton that permits a representation of the spin of the neutron without the Pauli-Fermi hypothesis of the neutrino, and its replacement with a longitudinal impoulsi propagated by the ether [21] that, while being compatible with neutrino experimsnts, permits far reaching advances in communication [22].

FINANCIAL SUPPORT
All participants, including auditors, are requested to have their participation approved by Prof. Christian Corda, or by Prof. A. Aringazin. Following their approval, participants are welcome to apply to the R. M. Santilli Foundation for financial support by contacting with their CV: Dr. Richard Anderson, Trustees, the R. M. Santilli Foundation, Email board@santilli-foundation.org.

Some of the open problems for which the Foundation has available research grants are: solution of isolinear differential equations; IsoNilpotency; representation of the Lie-Santilli isotheory; inclusion of exceptional algebras of the Tsagas unification of all simple Lie algebras of dimension N into one single Lie-Santilli isoalgebra with the same dimension; and other intriguing open mathematical problems (see the general review [19]).

NOTE ADDED ON AUGUST 1, 2013
Following the call for attention to the risk for our planet caused by the open problem of detecting antimatter asteroids, call presented in the recently published paper

AN INTRODUCTION TO
SANTILLI'S ISODUAL REPRESENTATION OF ANTIMATTER AND
THE ENSUING PROBLEM OF DETECTING ANTIMATTER ASTEROIDS
Richard Anderson, Anil A. Bhalekar, B. Davvaz, Arun Muktibodh,
Pradeep Muktibodh, Vijay M. Tangde, and Thomas Vougiouklis
Numta Bulletin, issue 6, January 2013
http://www.santilli-foundation.org/docs/Antimatter-2013.pdf

the Workshop shall dedicate a session in the classical representation of neutral antimatter body. The only methods known to the organizers at this writing are those permitted by Santilli isodual mathematics for exterior conditions of neutral or charged antimatter in vacuum and its isotopic covering for reversible interior conditions. Participants are warmly recommend to indicate any available alternative method for the representation of antimatter asteroids that, as such, are classical and neutral antimatter bodies.

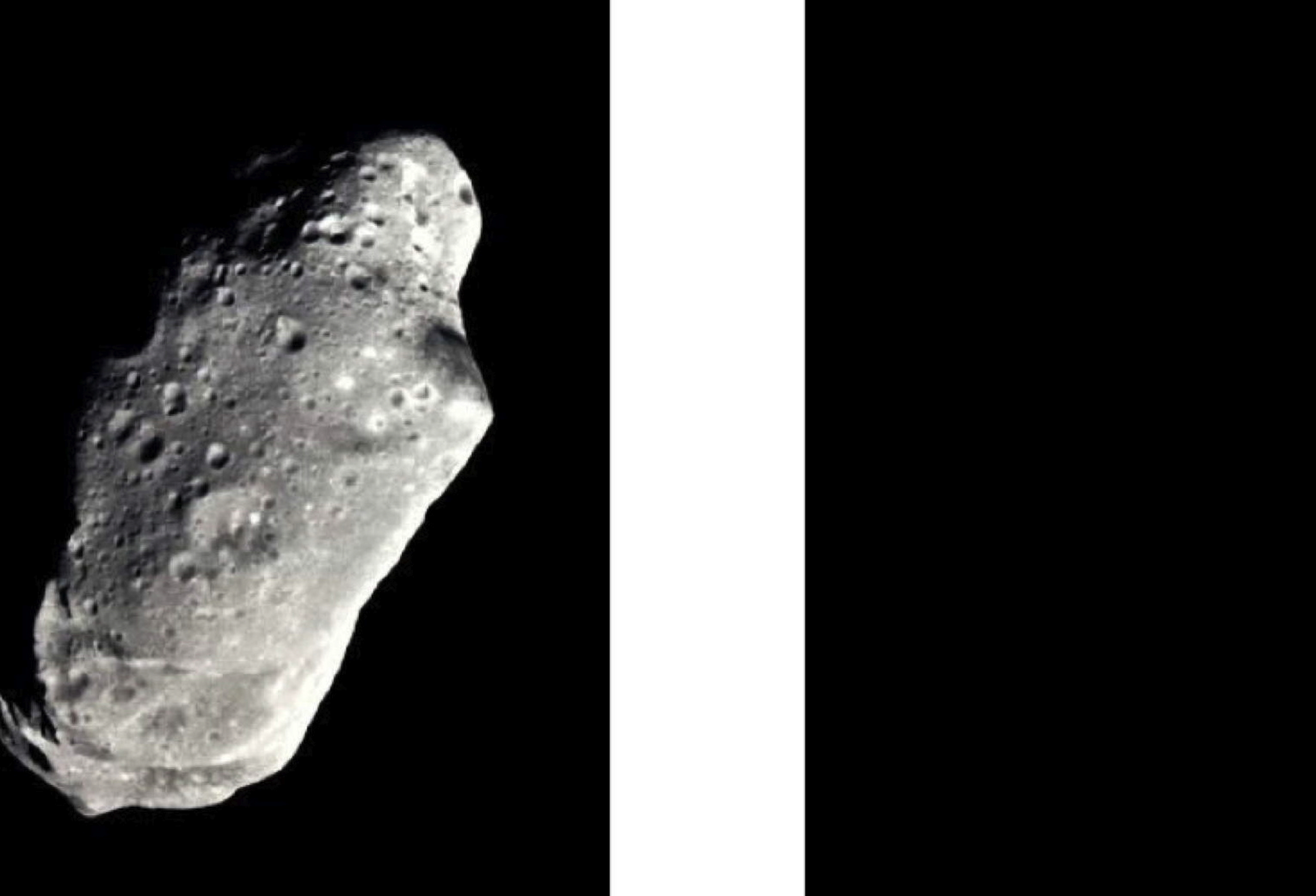
An illustration of our current inability to state with certainty that we are able to detect antimatter asteroids, since "matter light"(originating from our Sun) could be absorbed via annihilation-type processes when hitting a cold "antimatter asteroid," without the usual refraction of matter light on matter bodies. A call for systematic collegial studies of this open problem has been launched in the above quoted paper by R. Anderson et al. in view of the evidence that Earth has indeed suffered in the past devastation due to antimatter asteroids with ensuing paralysis of all communications due to the high excitation of Earth's atmosphere.

REFERENCES
[1] R. M. Santilli, Invited paper for the 2012 ICNAAM Conference, The American Institute of Physics, download
[2] R. M. Santilli, Algebras, Groups and Geometries 10, 273 (1993), download
[3] C. Corda, AIP, Conf. Proceed. 1479, 1013 (2012), download
[4] Chun-Xuan Jiang, Foundations of Santilli Isonumber Theory, International Aca- demic Press (2001), download
[5] R. M. Santilli, Intern. J. Modern Phys. D 7, 351 (1998), download
[6] J. V. Kadeisvili, Algebras, Groups and Geometries Vol. 9, 38 (1992), download
[7] R. M. Santilli, in Special Issue on Santilli's Isotopies, P. Vetro, Editor, Rendiconti Circolo Matematico Palermo, Suppl. 42 (1996), download
[8] ] D. S. Sourlas and G. T. Tsagas, Mathematical Foundation of the Lie-Santilli Theory, Ukraine Academy of Sciences (1993),download
[9] A. K. Aringazin, Algebras, Groups and Geometries 28, 299 (2011), download
[10] H. C. Myung and R. M. Santilli, Hadronic Journal 5, 1277 (1982). download
[11] R. M. Falcon Ganfornina and J. Nunez Valdes, Algebras, Groups and Geometries 20, 1 (2003), download
[12] R. M. Santilli, Foundation of Theoretical Mechanics, Springer-Verlag, Heidelberg, Germany, Vol. I, 1978, Vol. II, 1981
[13] R. M. Santilli, Elements of Hadronic Mechanics, Ukraine Academy of Sciences (1995), Vol. I download, Vol. II download
[14] R. M. Santilli, Isodual Theory of Antimatter with Application to Antigravity, Grand Unification and the Spacetime Machine, Springer 2001
[15] H. Ahmar, G. Amato, J. V. Kadeisvili, J. Manuel, G. West, and O. Zogorodnia, IJCMAE, in press download
[16] Y. Yang, J. V. Kadeisvili, and S. Marton Experimental Confirmations of the New Chemical Species of Santilli Magnecules, in press download
[17] Robert Brenna, Theodore Kuliczkowski, Leong Ying, " Advances in Physics, download
18] J. V. Kadeisvili, "The Rutherford-Santilli Neutron," Hadronic J. 31, 1 (2008), access
[19] I. Gandzha and J. Kadeisvili, New Sciences for a New Era, Sankata Printing Press, Nepal (2011), download
[20] R. M. Santilli, Foundations of Hadronic Chemistry, with Applications to New Clean Energies and Fuels, Kluwer Academic Publishers (2001).
[21] R. M. Santilli, "The etherino and/or the Neutrino Hypothesis?" Found. Phys. Vol. 37, p. 670 (2007)
www.santilli-foundation.org/docs/EtherinoFoundPhys.pdf
[22] R. M. Santilli, "Compatibility of super/sub-luminal speeds with Einstein's special relativity axioms." to appear
\http://www.santilli-foundation.org/docs/super-sub-luminal-speeds.pdf